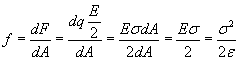The charge- and force distribution analysis of the lifter in vacuum
by Zoltan Losonc - courtesy Zoltan Losonc
Document source : http://feprinciples.true.ws/liftvac.htm

Purpose

The purpose of the following examination is to find out whether the asymmetrical electric forces could result in a reaction-less total force upon the lifter (as in the case of Forlov’s T-capacitor) in perfect vacuum, and explain the measured values at least partially. If there is such reaction-less force, then what is its magnitude? If there is no such force from this effect in vacuum (or negligible), then is there any possibility to obtain a resultant reaction-less force form electrostatic forces in the presence of air.

Initial assumptions

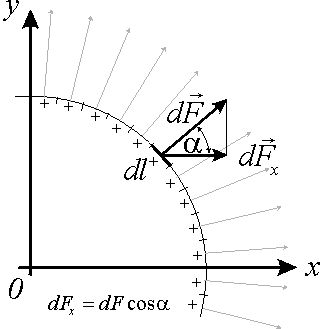
For the following examination we assume that the lifter consisting of a thin corona wire and a conducting plate with rounded edge facing the wire is much longer than its greatest cross sectional dimension, and it is in perfect vacuum with no other objects or external E-fields nearby. This assumption is needed to simplify the problem to a degree when it can be easily solved. The cross-section of the lifter in x-y plain is shown in fig 1.

Fig. 1.

Since the length of the lifter is usually much greater then its cross-sectional dimensions, its charge distribution and E-field will differ very little from the case of an infinitely long lifter (except in the proximity of the ends). The analysis of an infinitely long (in both z directions) lifter is easier because we can neglect the influence of the ends, but the results and conclusions will be also valid for real lifters of finite length with good approximation. After deriving the x component of the resultant force per unit length, the total force upon a real lifter can be calculated by multiplying this value with its length. For the calculations we use MKS system of measures.

Global description of the calculation

If there is electric charge on the surface of the bodies then electric field lines will originate and terminate in these charges. Since the electric field lines are also force lines (unlike the magnetic field lines) a force will attempt to pull these charges out of the surface in the direction of the E-field. We know further that the vector of E-field is always perpendicular to the surface of a conductor in electrostatics. The magnitude of this force per unit surface (or the electrostatic pressure) can be calculated with the formula:

(s - charge density on the surface, E – electric field intensity, e - dielectric constant of the surrounding medium). The explanation of this formula can be found in appendix 1.

To calculate the forces acting on the lifter, first we have to find the charge densities in each point on the surface of the conductors. Then dividing the whole surface into small segments we calculate the elementary forces on each of these segments. Since these forces are not parallel with the x-axis but perpendicular to the surface element, we have to calculate their x-components in order to get the thrust in x direction as shown on fig 2.

The program used for the analysis

In lack of a better alternative I have written a program for this special case to solve the problem. A variant of the collocation BEM method have been used to find the charge distribution, and then calculated the forces on each of the 4 parts of the lifter. The cross section of the examined geometry for this program is shown in fig 3.

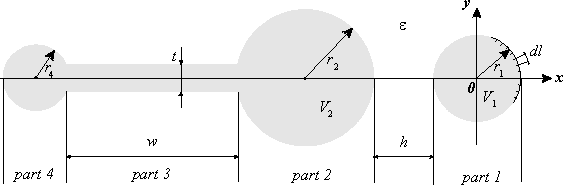
Fig. 3.

By changing the parameters shown on the drawing we can calculate the charge distribution and forces for different dimensions and voltages in search for the optimal proportions for the highest resultant force (if any). If the examined case does not have cylindrical edge in part 4, then we can take r₄ = t/2 to get semicircular edge of the plate. The accuracy of the result is mainly determined by the relative size of the elementary segment dl, which can be made enough small by choosing appropriately big number of elements n that cover the upper surface of the geometry (above the x-axis).

Testing the accuracy of the program

Before accepting the results generated by the computer as a valid solution, we have to find some way to develop trust in the accuracy of the program. There are several possibilities for this verification. Perhaps the easiest and most convincing is to calculate the specific capacity between two infinitely long cylinders from the obtained charge distribution, and to compare it with the analytically derived value. For the sake of this comparison the following input parameters create a geometry, which represents a very good approximation of two parallel infinitely long conducting cylinders with identical radius r₁ = r₂ = r and with D = r₁+ r₂+ h = 2r+ h distance between their axes.

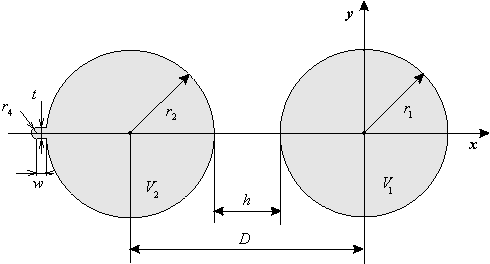
Fig. 4.

Table 1.

After giving the initial input parameters, the program slightly modifies them to insure integer number of segments on each part, so the calculations are made actually with the normalized parameters. The small relative dimensions of w, t and r₄ will transform the ‘tail’ portion into a sharp edge with high local charge density, but the additional charge and capacity from this edge will be negligible compared to the perfect cylinders, since the surface of the edge is very small.

To verify the accuracy of the charge distribution computed by the program, we calculate the capacity of the cylinders from these charge densities. This is done by a separate subroutine, which multiplies the local charge density in each segment with the length of the segment dl and adds up these values separately for both cylinders. The results will represent the total charge per unit length (along z-axis) on the cylinders. Since both of them have approximately identical radius, the capacity can be derived from these charges as C = q₁ / (V₁ - V₂). The second cylinder in the computer simulation has a little asymmetry caused by the ‘tail’ edge and slightly different radius; therefore we will not get identical charges for both cylinders. Although the difference is not significant, it is still more accurate if we use the charge on the 1^st cylinder for the calculation of the capacity.

For the above input parameters the program has given the following charge distribution and capacity:

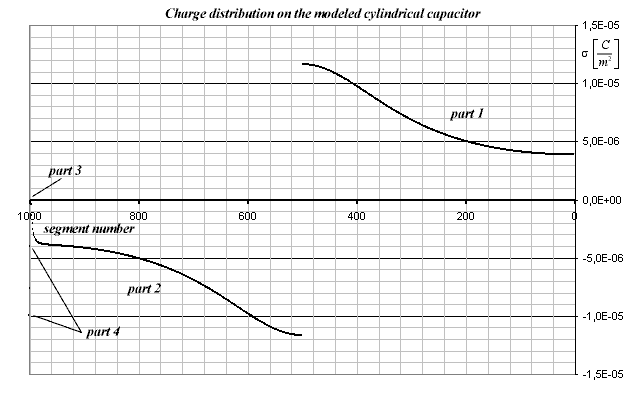
Diagram 1.

Table 2.

The next step is to calculate the capacity of these cylinders with the same parameters using the analytically derived exact formula that can be found in the electromagnetic textbooks:

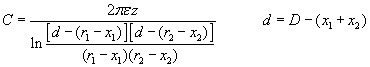
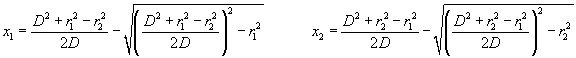
If we substitute the given (normalized) parameters into this formula the C_a=2,11219009187543E-11 value is obtained. Comparing the numerically and analytically derived values the error e = ( C_a – C_n ) / C_a * 100 % is only e = -1,59E-02%. This accuracy has been achieved with n = 1000 (the total surface divided into 2*1000 = 2000 segments), and it will be enough for our purposes.

The charge distribution and forces on a tested lifter in vacuum

Now let us see the charge distribution and calculated forces in perfect vacuum for a typical lifter (lifter 1) built by JL Naudin. The input parameters for this case are:

Table 3.

The following diagram shows the plotted coordinates of each segment’s center above the x-axis:

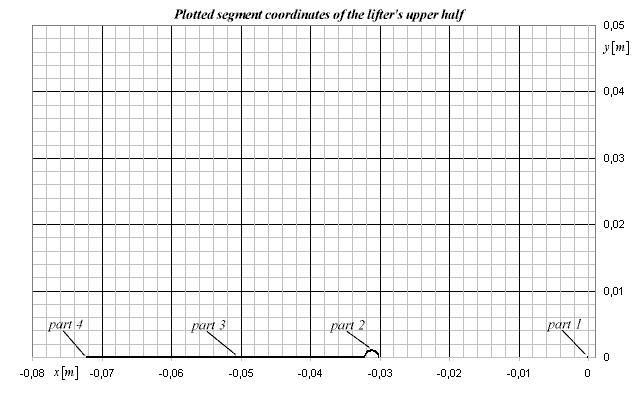
Diagram 2.

Since the cross-section of the lifter is symmetrical to the x-axis it is enough to calculate the charge distribution and forces only for the upper part. The lower part will have the same values mirrored below the x-axis, and the total force on the bodies will be 2-times the calculated forces for the upper half. Therefore only the upper part is visible in the diagram.

The charge distribution of this setup is shown on the following diagram:

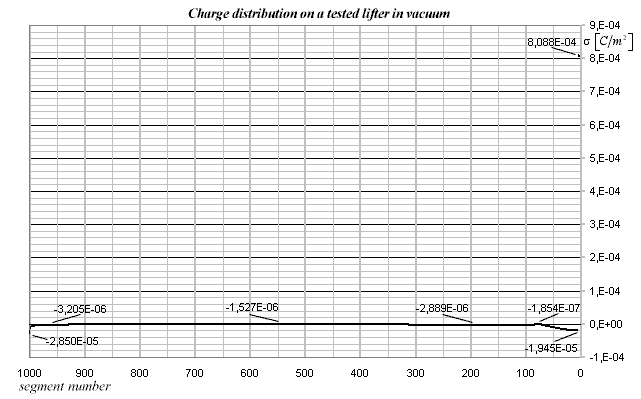
Diagram 3.

The numbers along x-axis represent the segment numbers in which the charge densities are calculated. Since the diameter of the wire and the thickness of the plate are much smaller than the width of the plate, even by dividing the upper surface into n = 1000 segments only the first 4 segments are in part 1, 71 in part 2, and only 2 segments in part 4; all the rest is in part 3. These big differences cause also huge differences in charge densities at different points on the lifter. To get a feel for the magnitude of the s obtained, you can calculate the intensity of the E-field on the surface of the conductor as E = s /e ₀  (e ₀ = 8.854E-12) and compare it with the E_d = 2,98E6 V/m disruptive critical E-field intensity of the air at normal pressure. This value is exceeded by an order of magnitude on the surface of the corona wire and also approached at the sharp edge of the plate. This causes the corona discharge in the presence of air, the leakage current and the ion wind. The highly ionized air around the corona wire builds a conducting space charge layer, and a virtual increase in wire diameter. So the calculated charge distribution and forces are not valid in the presence of air, because in that case we would have to calculate with the increased virtual corona wire diameter to take into account the effect of the space charge.

Using the above described method (based on electrostatic pressure) the program calculates the forces only upon the parts 1, 2 and 4, since the surface of the plate (part 3) is parallel with the x-axis and the vectors of E-field on the surface are parallel with the y-axis. This yields no force component in x direction and owing to the symmetry, the y components will cancel each other. The calculated forces on these parts are:

Table 4.

Although the resultant F in the second column is two orders of magnitude smaller than F2 it is still difficult to say immediately, whether this is a real reaction-less force or it is the calculation error that actually should be zero. We have good reason to take it to be the inaccuracy of the calculation, since the surface of the wire is divided into only 8 segments and the edge of the plate into 4 segments. Since the elementary forces in this method are proportional with the square of the local charge densities, any small error in local s  will be amplified. The error is further increased by the inaccuracy in calculating the x component of the forces on the wire and on the edge of the plate due to the rough segmentation.

To solve this dilemma the program has been extended with a subroutine, which calculates the forces using the Coulomb’s law and gives a more accurate final result. The third column shows the forces calculated this way. According to this method the program chooses a segment, and calculates the x-component of the E-field intensity created by the charges from all other segments at its center. Then multiplying it with the charge per unit length (in z direction) present in the chosen segment an elementary force is obtained. Calculating and summing up all these elementary forces, we get the total force (per unit length) in x direction. The resultant F in the third column is 1E13 times smaller than F2 and it is negligibly small. This confirms that the resultant force will tend towards zero as the accuracy of the calculation is increased.

By increasing the number of segments the accuracy should also increase. If we take n = 3000 (6000 segments covering the whole geometry) instead of n = 1000, we get the following results:

Table 5.

In this case 24 segments cover the wire and 12 the edge of the plate which gives higher accuracy. Comparing this table with the table 4. we can see that F in the second column approaches better the zero value, confirming the above conclusions. The non-zero value of F3 in the 3^rd column is explained in appendix 2.

The order of magnitude of the F₂ is the same as measured in the presence of air, but the F₁ is much greater than what is measured in the presence of air with disconnected armatures, and F₁ + F₃ + F₄ cancels the forward thrust of F₂ with high accuracy.

Conclusion

In vacuum: according to this analysis there is no resultant force upon the lifter in perfect vacuum resulting from the asymmetrical electric forces, or it is negligible compared to the value in the mN range measured in high vacuum of 1.333e-3 Pa by William B. Stein at Purdue University.

(Mr. Stein has measured at least 0.31 mN with 0.12 m long lifter at 17 kV. According to T. Townsend Brown’s letter from February 14, 1973 the thrust in vacuum is linear with the voltage. Since we have used 2.3 times higher voltage and 5 times longer lifter, we would expect a force of at least 2.3*5*0.31 mN = 3.65 mN. Even the higher value of F2 in the second column is an order of magnitude smaller than what is expected, based on measurements and it can not explain the measured phenomena.)

Mr. Stein has proved in his paper “Electrokinetic Propulsion: The Ionic Wind Argument” that the ionic wind effect can not explain the phenomena in high vacuum. Since neither the electric forces of the asymmetrical E-field can provide a magnitude of force that could explain the measured thrust in vacuum, this analysis confirms the theory that at high E-field intensities in vacuum an unknown electro-gravity force is responsible for the measured thrust.

In the presence of air: most of the thrust is provided by the electric forces between the dense space charge around the corona wire (causing a virtual increase of the wire diameter) and the cylindrical edge of the plate facing the wire. This causes the ion drift process described by Evgenij Barsoukov. Although the basic principles in his theory are correct, the quantitative analysis was based on unrealistic assumptions and the derived formula is not valid (it is not in conformity with the measurement results). Even if we could find a good approximate formula for this thrust based on ion drift process, it still assumes the validity of Newton’s 3^rd law; that means this force would be ineffective if the lifter would be fixed within a completely sealed box.

A further object of examination is to find out whether it is still possible to obtain a reaction-less resultant force-component from the electrical forces between a static space charge around the corona wire and the plate. The dependency of the trust from the voltage, from the wire diameter (real and virtual) and from the distance between armatures needs also to be clarified. These questions will be explored in the next update.

Appendix

1. The electrostatic pressure perpendicular to the surface of the conductor

According to Coulomb's law the force dF acting on a charge dq is dF = dqE . Since the E-field intensity on the surface of a conductor is
E = s /e  and  dq = s dA we might conclude that the force will be and the electrostatic pressure (dA – elementary surface). This is however not true.

The explanation for this is that the charges on the surface of a conductor are not in the form of an infinitely thin layer of charge, but the layer has a finite thickness. Therefore they build a thin layer of space charge below the surface as shown in the following figure:

1. 

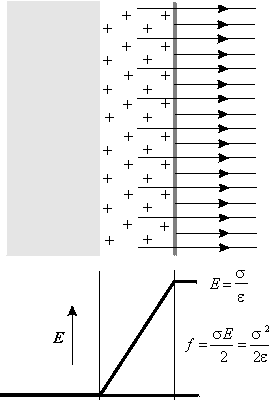
   Fig. 5.

The E-field intensity beneath the surface (around the charges) is not constant but it changes linearly from zero to E = s /e value on the surface (assuming constant space charge density). Thus the mean value of the electric field intensity in the region of the space charge is E/2, and the correct formula for the electric force per unit surface:

return

2. Explanation of the non-zero tangential force-component on the surface of the plate.

The fundamental rule of the electrostatics says that no tangential electric force component can exist on the conductor’s surface, since then the charges would move in the direction of the force (which is not a static case) until the equilibrium is attained. That means, since the program calculated a small negative tangential E-field and force F3, there should be an equivalent positive E-field and force acting on the charges within the examined segments that was not taken into account. This assumption is correct, because while calculating the E-field intensity at the center of the examined segment only the contribution of the charges present in other segments has been taken into account. However, since the space charge density (discussed in appendix 1.) in the thin layer beneath the surface is not homogenous along the surface, but it is increasing towards one end of the segment, it will create a ‘self-generated’ local E-field within that segment that will cancel the tangential E-field and force component. Taking into account the local tangential E-field during the calculation of the forces would overcomplicate the program and it is neglected; this causes the nonzero F3. By increasing the number of segments and further refining the program this error can be decreased to a negligible value.

return